#1
- Vector & Matrix Caluclation
- Unit Vectors
- Identity Matrix
- Determinant
- Inverse matrix
- 벡터와 매트릭스의 기본 연산
- Span, Basis, Rank
- Linear Projection
#2
- 분산과 표준편차
- 공분산
- 상관계수
- Vector Transformation
- EigenVector , EigenValue
- PCA
- High dimension Data와, 이로 인한 이슈
- Feature Extraction / Selection
#3
- Scree Plot
- Supervised / Unsupervised Learning
- K-means clustering
Variance 분산
: 분산이란 데이터가 얼마나 퍼져있는지에 따른 정도를 나타낸 것이며 관측값에서 평균값을 뺀 것이다.
standard deviation 표준편차
: 표준편차란 자료의 관찰값이 얼마나 흩어져 있는지를 나타내는 값이며, 분산을 제곱근한 것이다.
수식:
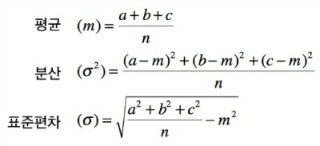
Data를 다룰때 주의할 점
: 모집단의 분산(σ^2)을 구할때 모집단 분산은 모집단의 Parameter이고, 샘플의 분산(s^2)을 구할때 샘플 분산은 샘플의 Statistic(통계량)이기 때문에 주의해야한다. 즉, (s^2)는 (σ^2)의추정치이다.
위의 수식은 모집단의 분산을 구하는 방법이다. 일반적으로 샘플의 분산 (s^2)을 구할때는 분모에 n이 아닌 n-1을 대입해야한다. 그렇기 때문에 자유도 설정을 바꿔줘야한다. ex) (σ^2 of dof : 1->s^2 of dof : 0)
Covariance 공분산
: 1개의 변수 값이 변화할 때 다른 변수가 어떠한 연관성을 나타내며 변하는지를 측정한것.
공분산 크기에 따른 그래프

공분산을 구할 때 공분산이 클수록 두 변수간의 연관성이 나타나는데 변수간의 Scale이 다르다면 공분산은 실제 변수간의 연관성이 적어질 것이다. 즉 변수의 Scaling을 수행 해야할 것이다
Correlation coefficient 피어슨 상관계수
: 위에서 공분산을 스케일링 하기 위해 공분산을 두 변수의 표준편차로 각각 나눠주면 스케일 조정이 가능하다.
그리고 이것을 상관계수라고 부른다. 상관계수는 -1~1까지로 정해진 범위의 값만을 가지며 선형 연관성이 없을 경우 0에 근접한다. 상관계수는 데이터의 평균이나 분산의 크기에 영향을 받지 않는다.
상관계수는 일반적으로 소문자 r 로 표현한다.
Cor(x,y) = r = (Cov(x,y) / (σx*σy))
Vector transformation 벡터 변환
: 선형 변환을 뜻하는 것으로 임의의 두 벡터를 스칼라 값을 곱하거나 더하는 것을 의미한다.
목적
: Vector Transformation은 곱하고 더하는 것만의 Transformation이다. 즉, Matrix와 Vector의 곱으로 표현 할 수 있다.
임의의 Vector를 다른 내부의 Vector 변환하는 과정은 특정 Matrix를 곱하는 것과 동일한 과정이다.
즉, Matrix를 곱하는 것을 통해 Vector라는 데이터를 다른 위치로 옮긴다.
예시
:
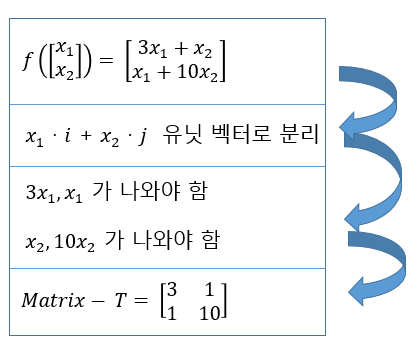
Eigenvector 고유벡터, 고유값 (Eigenvalue) [Reference 다크프로그래머]
: 행렬 A를 선형변환으로 봤을 때, 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터를 고유벡터(eigenvector)라 하고 이 상수배 값을 고유값(eigenvalue)라 한다.
λ는 [행렬 A의 고유값], v는 [행렬 A의 λ에 대한 고유벡터]이다.

기하학적으로 봤을 때, 행렬(선형변환) A의 고유벡터는 선형변환 A에 의해 방향은 보존되고 스케일(scale)만 변화되는 방향 벡터를 나타내고 고유값은 그 고유벡터의 변화되는 스케일 정도를 나타내는 값이다.

예를 들어 지구의 자전운동과 같이 3차원 회전변환을 생각했을 때, 이 회전변환에 의해 변하지 않는 고유벡터는 회전축 벡터이고 그 고유값은 1이 될 것이다.
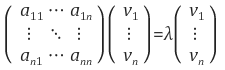
PCA (Principle Component Analysis) 기본 구성 요소 분석
: 고차원 데이터를 효과적으로 분석 하고 시각화 하기 위한 기법으로 고차원 데이터를 낮은 차원으로 차원축소한다.
원래 고차원 데이터의 정보(==분산)를 최대한 유지하는 벡터를 찾고, 해당 벡터에 대해 데이터를 Linear Projection한다.
PCA의 특징 :
데이터에 대해 독립적인 축을 찾는데 사용 할 수 있다.
데이터의 분포가 정규성을 띄지 않는 경우 적용이 어렵다.
-이 경우는 커널 PCA 를 사용
분류 / 예측 문제에 대해서 데이터의 라벨을 고려하지 않기 때문에 효과적 분리가 어렵다.
-이 경우는 PLS 사용
즉, PCA를 통해 차원 축소를 할때 데이터의 정보인 분산이 큰 차원을 사용해야 한다.
왜 고차원일때 문제가 생긴다는 것일까?
고차원의 문제 (The Curse of Dimensionality)
: Feature가 많은 데이터셋을 분석하거나 모델링할때 생기는 문제점들.
Feature가 2개,3개 즉 2차원, 3차원 까지는 2D, 3D 모델링을 통해서 시각화 하고 데이터를 분석할 수 있다.
하지만 10차원 20차원이 된다면 얘기는 달라진다 이를 분석하기도 힘들 뿐만 아니라 시각화를 한다고 하더라도 더 복잡하기 때문이다.
이렇기 때문에 데이터의 일부를 제한하더라도 데이터의 의미 파악에는 큰 변화가 없다면 많은 수의 Feature를 사용하는것이 비효율적이라고 볼 수 있다.
->
샘플에 비해 Feature가 너무 많은 경우 OverFitting의 문제가 발생한다.
Feature의 수를 P, sample의 수를 N이라 할 때P >= N일 경우 OverFitting의 발생 가능성이 높다고 한다..
그렇다면 중요한 Feature를 선택하기 위해 어떤 방법을 써야할까?
Feature Selection 과 Feature Extraction
: Feature Selection : 덜 중요한 Feature를 제거 하는 방법
Feature Extration : 기존의 있는 Fature나 기존의 Feature를 조합한 Feature를 사용함.

| Selection | Extraction | |
| 장점 | 선택된 feature 해석이 쉽다. | feature 들간의 연관성 고려됨. feature수 많이 줄일 수 있음 |
| 단점 | feature들간의 연관성을 고려해야함. | feature 해석이 어려움. |
| 예시 |
LASSO, Genetic algorithm 등 | PCA, Auto-encoder 등 |
Reference
다크프로그래머 darkpgmr.tistory.com/105
'CodeStates' 카테고리의 다른 글
| [머신러닝 - 선형모델]#2 (0) | 2021.04.08 |
|---|---|
| [머신러닝 - 선형모델]#1 (0) | 2021.04.07 |
| [선형대수학] #1 (0) | 2021.03.21 |
| [통계] #3 (0) | 2021.03.15 |
| [통계] #2 (0) | 2021.03.14 |



