목차
#1
- Vector & Matrix Caluclation
- Unit Vectors
- Identity Matrix
- Determinant
- Inverse matrix
- 벡터와 매트릭스의 기본 연산
- Span, Basis, Rank
- Linear Projection
#2
- 분산과 표준편차
- 공분산
- 상관계수
- Vector Transformation
- EigenVector , EigenValue
- PCA
- High dimension Data와, 이로 인한 이슈
- Feature Extraction / Selection
#3
- Scree Plot
- Supervised / Unsupervised Learning
- K-means clustering
#1
#1
Vector & Matrix Caluclation
Vector Caluclation 벡터연산
벡터의 곱셈
백터의 곱셈은 내적과 외적이 있다.
이를 설명하기 위해 위키독스에서의 설명을 참고하겠다.
벡터의 내적
먼저 내적을 설명하겠다.
내적은 벡터를 마치 수처럼 곱하는 개념이다.
벡터에는 방향이 있으므로, 방향이 일치하는 만큼만 곱한다. 예를 들어 두 벡터의 방향이 같으면, 두 벡터의 크기를 그냥 곱한다. 두 벡터가 이루는 각이 90도일 땐, 일치하는 정도가 전혀 없기 때문에 내적의 값은 0이다. 내적은 한 벡터를 다른 벡터로 정사영 시켜서, 그 벡터의 크기를 곱한다.

내적의 기호는 가운데 점을 찍는 것(⋅)이고, 벡터의 크기를 절대값으로 표시하면, 내적의 값은 다음과 같다.

또한 벡터의 내적은 각 구성요소를 곱한후에 더한 합과 같다.
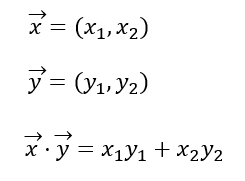
벡터의 내적의 결과값은 벡터가 아닌 스칼라이다.
벡터의 크기(norm, magnitude, length)

벡터의 외적
이제 외적을 설명하겠다.
외적의 결과값은 벡터인데, 방향은 곱하는 두 벡터에 수박하고, 크기는 두 벡터가 이루는 정사각형의 넓이이다. 외적의 연산 기호는 크로스이다. 외적의 크기(절대값)만 나타내보면, 다음과 같다.
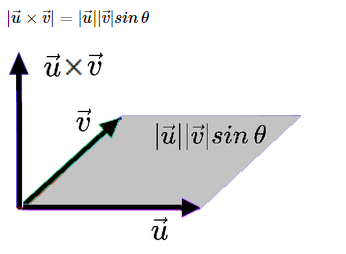
스칼라 : 단일 숫자로, 값을 저장 할때에는 일반적으로 소문자를 이용한다. 실수와 정수 모두 포함된다.
벡터 : 컴포넌트라고 불리는 n개의 원소를 가지는 순서가 있는 모음을 n차원 벡터라고부르고 일반적으로 위에 (→)문양을 갖는다.
데이터 사이언스 관점에서는 벡터의 길이는 벡터의 차원수와 동일하다고 볼 수 있다.

Matrix Caluclation 행렬 연산
행렬의 곱셈
행렬의 곱셈에 대해서는 아래와 같이 위키백과의 글을 인용하겠다.

행렬 곱셈을 위해선 첫째 행렬의 열 갯수와 둘째 행렬의 행 갯수가 동일해야한다. 곱셈의 결과 새롭게 만들어진 행렬은 첫째 행렬의 행 갯수와 둘째 행렬의 열 갯수를 가진다.

벡터의 직교(orthogonality) 확인
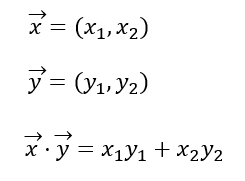
이때의 값이 0이 되면 벡터의 내적은 0이 된다.
Unit Vectors (단위벡터)
: 단위 길이 1을 갖는 모든 벡터
벡터의 정규화를 통해 단위 벡터를 구하는 방법은
단위벡터 v = 벡터 v / 벡터 V의 크기
ex) v = (4,3)일때

또한 모든 벡터는 단위벡터의 조합으로 표기 된다.
v = [10, 15]
= [1, 0] 10 + [0, 1] 15
= 10 · i + 15 · j
Determinant 행렬식
: 모든 정사각 행렬이 갖는 속성으로 det(A) 또는 |A|로 표기된다. 2x2 매트릭스를 기준으로, 행렬식은
AD-BD로 계산 가능하다.

|x| = AD-BC
Inverse matrix 역행렬
: 행렬 A의 역행렬은 A와 곱해서 항등행렬 E가 나오는 행렬을 A의 역행렬이라 정의한다.

위 식과 같이 A와 곱해서 E가 나오게 하는 행렬 B를 A의 역행렬이라고 하고 A-1로 표기한다.

이때 역행렬이 없는 특이 행렬을 singular matrix 라고 부른다.
행렬이 직사각행렬이라면 역행렬은 존재하지 않는다. 하지만 행렬이 정사각 행렬이라도 역행렬은 있을 수도 있고 없을 수도 있다.
벡터의 선형관계와 비선형관계
두개 이상의 벡터가 한 선상에 존재할 경우 이 벡터들을 아무리 조합해도 선 외부에서의 벡터가 생성 되지 않기 때문에 이 벡터들은 선형관계에 있다고 말할 수 있다.
이와 반대로 두개이상의 벡터가 서로 같은 선상에 있지 않다고 한다면 주어진 공간에서의 모든 벡터들을 이 벡터를 이용해 만들어 낼 수 있다. 예를 들어 비선형관계의 벡터2가지가 있다고 하면 평면에서의 모든 벡터들을 이 벡터를 이용해 만들어 낼 수 있다. (R^2)라고 한다.
Span
: 주어진 두 벡터의 합이나 차의 조합으로 만들 수 있는 모든 벡터의 집합이다.

Basis
:(일종의 Span 역개념으로)벡터 공간 V에서 V라는 공간을 채울 수 있는 선형 관계에 있지 않은 벡터들의 집합이다.
예를 들자면 위의 그림에서 2개의 벡터 (빨강, 파랑)는 벡터 공간 R^2 의 basis이다.
Orthogonal Basis
: 기존 Basis 개념에 추가적으로 직교한다는 조건이 붙는다. 주어진 공간을 채울 수 있는 서로 수직인 벡터를 뜻한다.
Rank
: 앞서 계속해서 나왔던 R^2에서의 R은 Rank를 뜻한다.
이는 Matrix의 열을 이루고 있는 벡터들로 만들 수 있는 공간의 차원(Span)이다.
Matrix의 행과 열을 이루고 있는 벡터들 가운데 선형 관계가 있을수도 있기 때문에 일반적인 Matrix의 차원과는 다를 수 있다. 여러가지의 Rank 확인법이 있지만 대표적으로 가우시안 소거법이 있다.
가우시안 소거법을 통한 Rank 산출

Linear Projection

기존의 방식으로는 Data 표현을 위해 x,y라는 2개의 Feature가 필요했다가 Linear Projection을 이용해 x만의 feature를 사용하게 된다면, Loss값이 발생하더라도 메모리등의 이득이 더 크기 때문에 사용한다.
Reference
위키백과 : ko.wikipedia.org/wiki/%ED%96%89%EB%A0%AC_%EA%B3%B1%EC%85%88
'CodeStates' 카테고리의 다른 글
| [머신러닝 - 선형모델]#1 (0) | 2021.04.07 |
|---|---|
| [선형대수학]#2 (0) | 2021.03.22 |
| [통계] #3 (0) | 2021.03.15 |
| [통계] #2 (0) | 2021.03.14 |
| [통계] #1 (0) | 2021.03.14 |



